Physicists Crack Three-Body Problem Using "Drunkard's Walk"

A physics problem that has plagued science since the days of Isaac Newton is closer to being solved, say a pair of Israeli researchers. The duo used "the drunkard's walk" to calculate the outcome of a cosmic dance between three massive objects, or the so-called three-body problem, Ashley Hamer reported for Live Science.

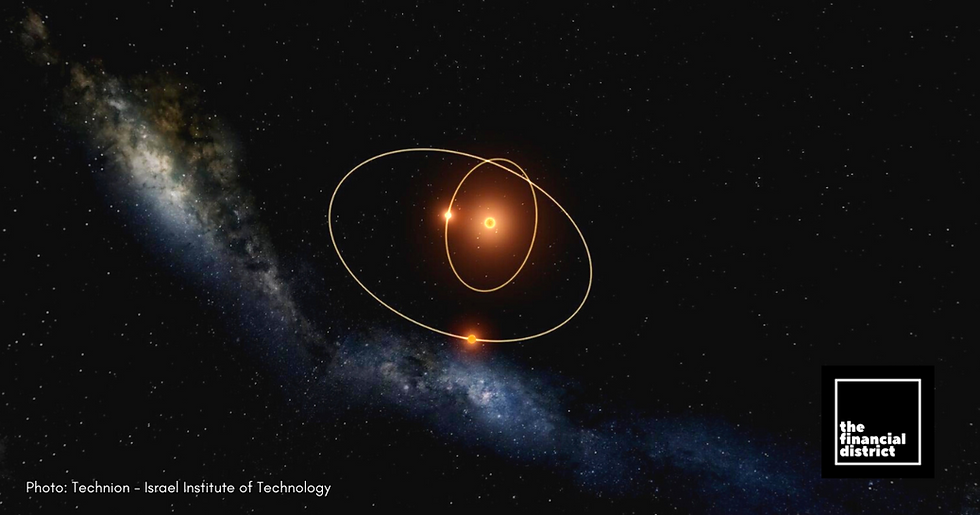
Photo Insert: Scientists used the frustrating unpredictability of the three-body problem to their advantage.

For physicists, predicting the motion of two massive objects, like a pair of stars, is a piece of cake. But when a third object enters the picture, the problem becomes unsolvable. That's because when two massive objects get close to each other, their gravitational attraction influences the paths they take in a way that can be described by a simple mathematical formula.

But adding a third object isn't so simple: Suddenly, the interactions between the three objects become chaotic. Instead of following a predictable path defined by a mathematical formula, the behavior of the three objects becomes sensitive to what scientists call "initial conditions" — that is, whatever speed and position they were in previously.

Any slight difference in those initial conditions changes their future behavior drastically, and because there's always some uncertainty in what we know about those conditions, their behavior is impossible to calculate far out into the future.

In one scenario, two of the objects might orbit each other closely while the third is flung into a wide orbit; in another, the third object might be ejected from the other two, never to return, and so on.

In a paper published in the journal Physical Review X, scientists used the frustrating unpredictability of the three-body problem to their advantage. "[The three-body problem] depends very, very sensitively on initial conditions, so essentially it means that the outcome is basically random," said Yonadav Barry Ginat, a doctoral student at Technion-Israel Institute of Technology who co-authored the paper with Hagai Perets, a physicist at the same university.

"But that doesn't mean that we cannot calculate what probability each outcome has." To do that, they relied on the theory of random walks — also known as "the drunkard's walk."

The idea is that a drunkard walks in random directions, with the same chance of taking a step to the right as taking a step to the left. If you know those chances, you can calculate the probability of the drunkard ending up in any given spot at some later point in time.

WEEKLY FEATURE : MVP Group Keeps Lights On During Pandemic